Coin Collecting Problem Dynamic Programming

Please help with this in c. It is possible to trace the computations backwards to get an optimal path.

Coin Collecting Problem Dynamic Programming Youtube

If Fi-1 j Fi j-1 an optimal path to cell i j must come from the adjacent cell on the left.

Coin collecting problem dynamic programming. A robot located in the upper left cell of the board needs to collect as many of the coins as possible and bring them to the bottom right cell. On each step the robot can move either one cell to the right or one cell down from its. The robot can only move from left to right or from top to down at a time.

A robot travels from the upper left corner to the bottom right corner collecting coins. The Coin Change Problem is considered by many to be essential to understanding the paradigm of programming known as Dynamic Programming. Our function is going to need the denomination vectors of coin d the value for which change has to be made n and number of denominations we have k or number of elements in the array d ie COIN-CHANGE d n k.

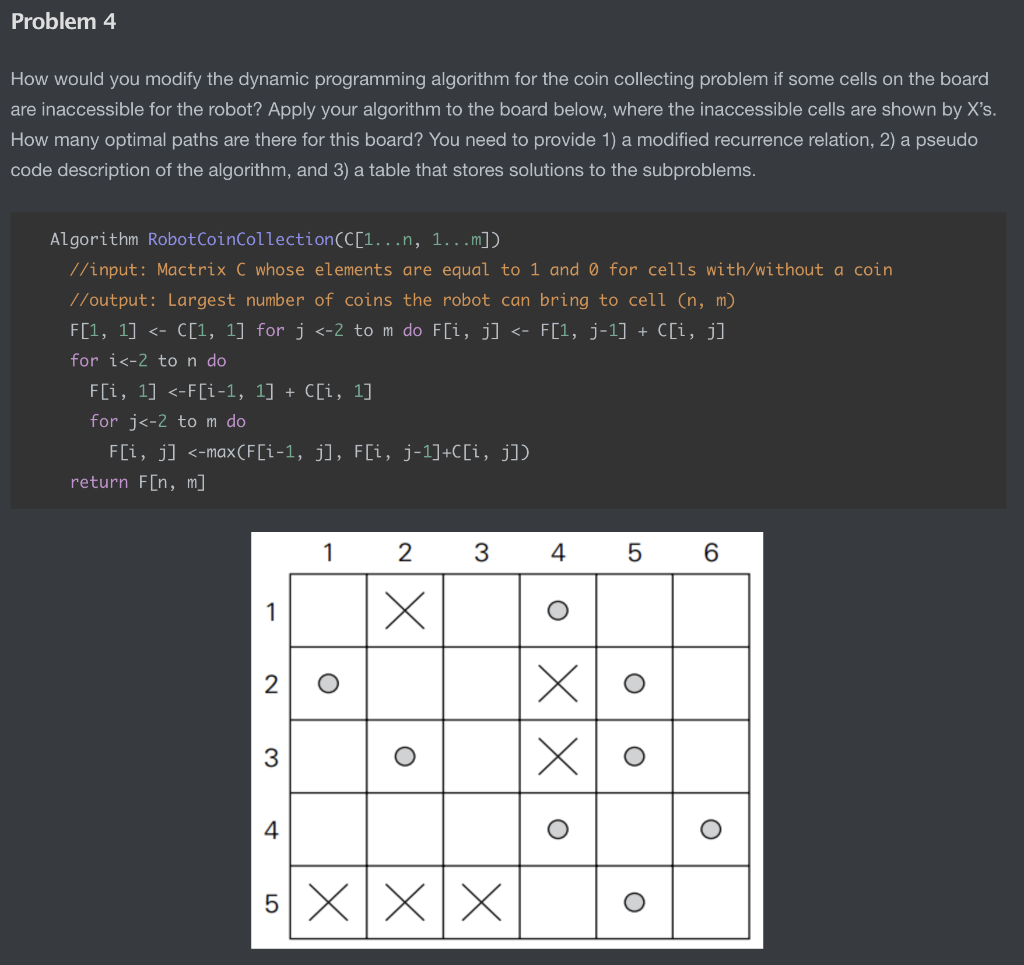
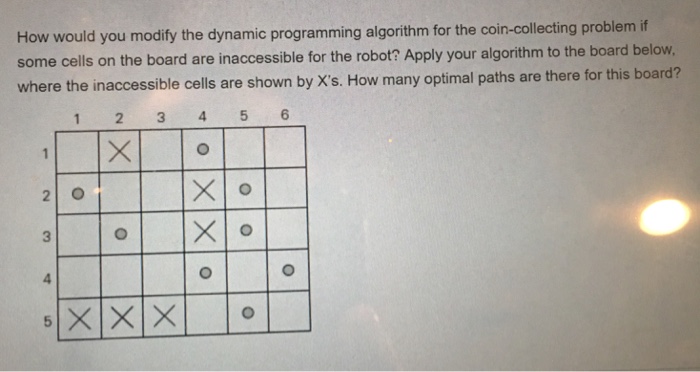
Dynamic Programming Solution for the Coin Collecting Problem. The coin-collecting problem if some cells on the board are inaccessible for the robot a Explain in words how this algorithm is different from the ordinary one. How would you modify the dynamic programming algorithm for the coin- collecting.

For those who dont know about dynamic programming it is according to Wikipedia. Write a program to solve the Robot coin-collecting problem by dynamic programming algorithm. The coin change problem is to find the minimum number of coins required to get the sum S.

If Fi-1 j Fi j-1 an optimal path to cell i j must come down from the adjacent cell above it. Robot coin collecting problem in a 2-d grid. Write a program to solve the Robot coin-collecting problem by dynamic programming algorithm.

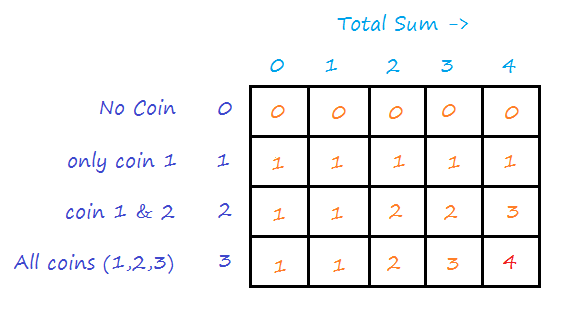
Robot Coin Collection-Dynamic Programming Introduction Dynamic problem is define as breaking down an optimization problem into sub problem and combine the solution of each overlapped sub problem. Lecture 9 Dynamic Programming 7 15 Solution to the coin-collecting problem cont Fi j maxFi-1 j Fi j-1 c ij for 1 i n 1 j m where c ij 1 if there is a coin in cell ij and c ij 0 otherwise F0 j 0 for 1 j m and Fi 0 0 for 1 i n. The two often are always paired together because the coin change problem encompass the concepts of dynamic programming.

Several coins are placed in cells of an n m board no more than one coin per cellA robot located in the upper left cell of the board needs to collect as many of the coins as possible and bring them to the bottom right cell. Robot Coin Collection Problem DYNAMIC PROGRAMMING 0 This is a classic DP question where there is a nxm board which has coin placed on some of the squares. Apply your algorithm to the board size 9 by 9 where the following cells have coins CELL Coin Amount 41 51 91 12 32 42 162 23 33 1431 74 194 35 45 55 75 95 36 66 86 196 77 87 97 18 38 178.

Code for Coin Change Problem We are going to use the bottom-up implementation of the dynamic programming to the code. B Write pseudocode for this modified algorithm. The first is a naive solution a recursive solution of the coin change program and the second is a dynamic solution which is an efficient solution for the coin change problem.

Computer Science questions and answers. Query is from Coin Change Problem in chapter. Example for dynamic programming.

It had no major release in the last 12 months. When the robot visits a cell with a coin it always picks up that coin. Robot Coin Collection Problem.

Apply your algorithm to the board size 9 by 9 where the following cells have coins CELL Coin Amount 41 51 91 12 32 42 162 23 33 1431 74 194 35 45 55 75 95 36 66. Dynamic-Programming-Coin-Collection has a low active ecosystem. This problem can be solved using _____ a Greedy algorithm b Dynamic programming c Divide and conquer d Backtracking This question was addressed to me by my school principal while I was bunking the class.

On each step the robot can move either one cell. CPS 616 DYNAMIC PROGRAMMING 8 - 3 EXAMPLE 3. There are two solutions to the coin change problem.

COIN-COLLECTING PROBLEM Problem Several coins are placed in cells of an n m board. On each step the robot can move either one cell to the right or one cell down from its current location. It has 1 stars with 0 forks.

1 2 3 4 5 6 1 2 3 4 5 16 Other Examples of DP Algorithms. Coin-collecting Problem How would you modify the dynamic programming algorithm for. The time complexity of the coin change problem is in any case nc and the space complexity is nc n.

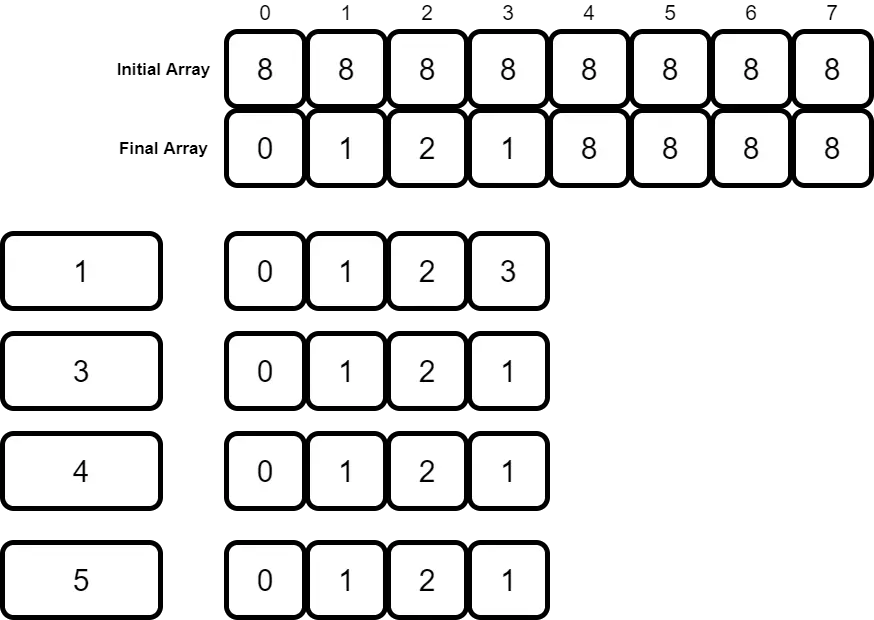
The algorithm should have two inputsC1n1m that encodes the. Coin-Collecting Problem Tracing back the optimal path. Design an algorithm to find the maximum number of coins the robot can collect and a path it needs to follow to do this.

Coin Collecting Problem Youtube